Current work
Here is a brief summary of my research projects. Please feel free to reach out if you are interested in details.
See also my ORCID or G-Scholar profiles for a full list of papers.
Quantum computing for discrete optimization: a highlight of three technologies.

Summary: presenting a practice-focused, OR scientist’s perspective on quantum optimization by highlighting three specific quantum technologies applied to three classical discrete optimization problems.
[ More details ]
Quantum optimization has emerged as a promising frontier of quantum computing, presenting a novel numerical approach to mathematical optimization problems. The key goal of this work is to facilitate inter-disciplinary research between the operations research (OR) and quantum computing communities by providing an OR scientist’s perspective on selected quantum-powered methods for discrete optimization. We consider three classical optimization problems, the Traveling Salesperson Problem, Weighted Maximum Cut, and Maximum Independent Set, to illustrate several approaches corresponding to different types of quantum hardware available on the market. Having a general OR audience in mind, we attempt to provide some intuition behind each approach along with key references, describe the corresponding high-level workflow, and highlight crucial practical considerations. In particular, we emphasize the importance of the problem formulations and device-specific configuration, and their effects on the amount of resources necessary for the computation (number of qubits and the related runtime). These points are illustrated using a series of experiments on quantum processing units of three types: an analog device from QuEra, a quantum annealer from D-Wave, and a gate-based device from IBM .
🖊️ Authors: A. Bochkarev, R. Heese, S. Jäger, P. Schiewe, A. Schöbel.
💬 Presentations: GOR-2023 (Hamburg, DE), GOR WG “Simulation und Optimierung komplexer Systeme” 2023 (Ingolstadt, DE), MIC-2024 (Lorient, FR).
💻 Software stack: Python (qiskit, D-Wave’s Ocean, aws/bracket), R/ggplot, Gurobi solver, bash, make.
Bayesian optimisation with improved information sharing for the variational quantum eigensolver

Summary: analyzing Bayesian optimization framework in the context of VQE with information sharing empirically. A BSc work by Milena Röhrs. (Co-supervised)
[ More details ]
This work presents a detailed empirical analysis of Bayesian optimization with information sharing (BOIS) for the variational quantum eigensolver (VQE). The method is applied to computing the potential energy surfaces (PES) of the hydrogen and water molecules. We performed noise-free simulations and investigated the algorithms’ performance under the influence of noise for the hydrogen molecule, using both emulated and real quantum hardware (IBMQ System One). Based on the noise free simulations we compared different existing information sharing schemes and proposed a new one, which trades parallelisability of the algorithm for a significant reduction in the amount of quantum computing resources required until convergence. In particular, our numerical experiments show an improvement by a factor of 1.5 as compared to the previously reported sharing schemes in H2 , and at least by a factor of 5 as compared to no sharing in H2O. Other algorithmic aspects of the Bayesian optimisation, namely, the acquisition weight decrease rate and kernel, are shown to have an influence on the quantum computation (QC) demand of the same order of magnitude.
🖊️ Authors: Milena Röhrs, Alexey Bochkarev, Arcesio C. Medina
An RL-powered heuristic for Dynamic Shortest-Path Interdiction
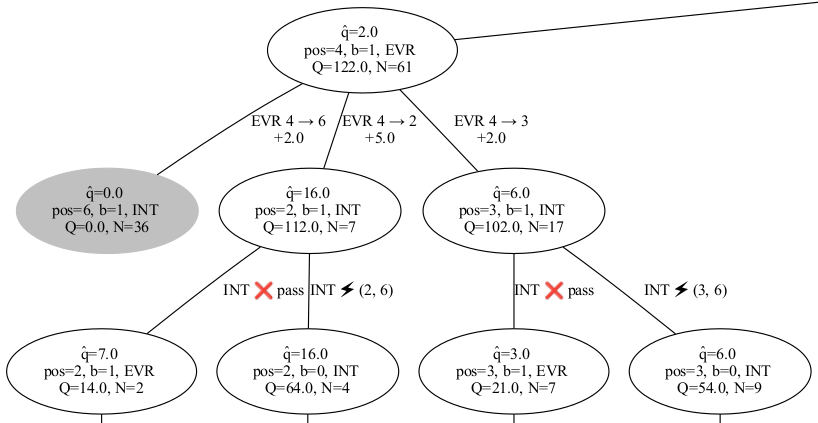
Summary: Designing algorithms to “play the game” of Dynamic Shortest-Path Interdiction (which is NP-hard). We are trying to explore the problem state space using the techniques involving random simulations and reinforcement learning.
[ More details ]
We are considering a dynamic game between two agents, “Evader” and “Interdictor”, over a directed weighted graph. The purpose of the Evader is to traverse a graph between “source” and “terminal” nodes at the minimum possible cost, given the other player’s actions. The “Interdictor” is seeking to maximize the Evader’s cost by “attacking” certain number of edges of the graph (which results in the arc cost increasing by a pre-defined amount). The players take turns, where the Evader’s turn implies traversal of an arc, and the Interdictor’s turn is either an attack or a pass. This variant of the game is known to be NP-hard, and an exact algorithm boils down to enumerating all the relevant states in a dynamic programming fashion.
While existing research discusses bounds for the optimal game cost, the literature on heuristics (algorithms that would actually play that game, or propose a policy for the players) has been generally lacking. We look to fill in this gap by leveraging some ideas from the realm of simulations and game playing research.
🖊️ Authors: Alexey Bochkarev, J. Cole Smith.
💬 Presentation: INOC-2022 in Aachen. See also Book of Abstracts, Session 4B (Interdiction), p. 129.
💻 Software stack: Julia, graphviz (dot), R/ggplot, PBS, make.
On collections of BDDs and “order-associated” diagrams.
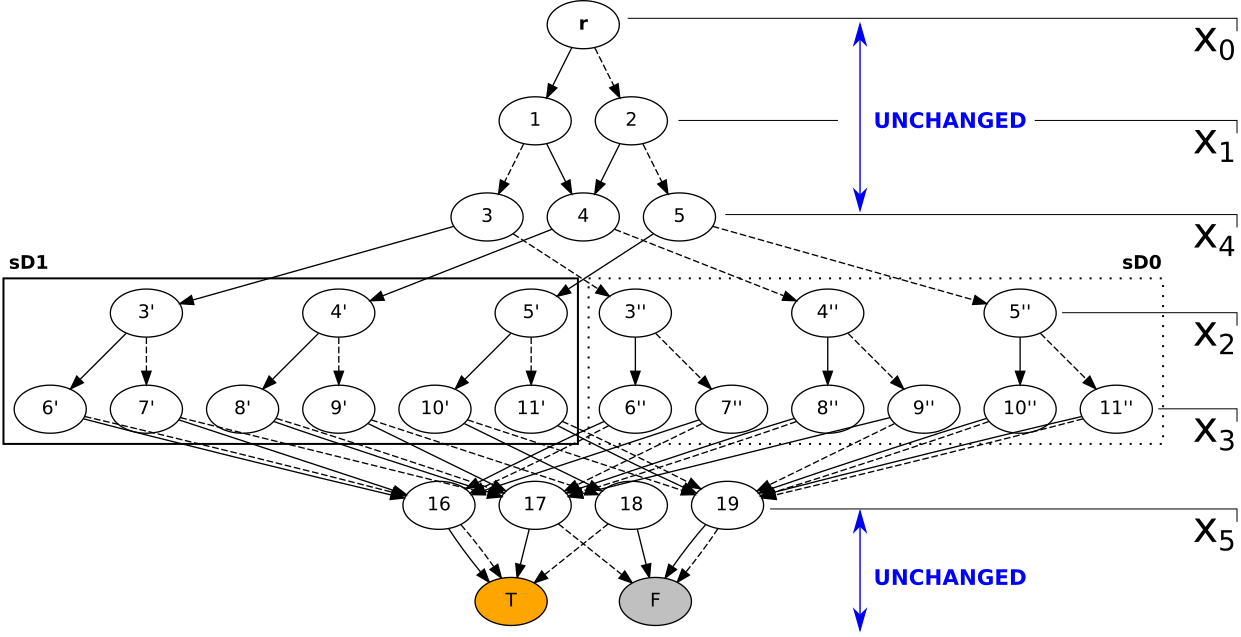
Summary: Designing a heuristic to find a “good” shared order of layers for a pair of Binary Decision Diagrams (BDDs) and applying it to build an exact solution to a hard optimization problem: a variant of facility location.
[ More details ]
The project focuses on Binary Decision Diagrams and their applications in optimization. This data structure was developed to efficiently manipulate Boolean functions, and sometimes it seems handy to represent a “logical” (binary) constraint as a diagram. So, some optimization problems can be naturally reformulated as linked network flows through a collection of diagrams (and we are looking for a “Consistent path” through several diagrams). Informally speaking, the latter can be solved relatively easily if the diagrams have their layers in the same order. Good order of layers may make a diagram small, but in a bad case the size of the diagram grows exponentially. Finding a best order of layers is NP-hard, even for a single diagram. The project is structured into two large, more or less independent parts.
First, we build a heuristic to “align” the diagrams. The central idea is simple: when we swap two adjacent layers in a diagram, their size change. But instead of working with the original diagrams, which can be computationally expensive, we can just keep track of the upper bounds on the layer sizes. This gives rise to a smaller auxiliary problem that sometimes does allow to find good shared order of layers in reasonable time.
In the second part of the project we actually use this idea to attack a hard combinatorial problem, a variant of the facility location. We demonstrate how to parameterize the problem using a collection of BDDs and compare several ways to obtain an (exact) optimal solution, revealing that Consistent Path representation along with the proposed “alignment” heuristic might allow to obtain some performance benefits (especially when we’d need to re-solve the problem with different numerical data) and sensitivity information.
🖊️ Authors: Alexey Bochkarev and J. Cole Smith.
💬 Presentation: INFORMS Annual Meeting 2020.
💻 Software stack: Python, R/ggplot, graphviz (dot), Gurobi solver, PBS, GNU parallel, bash, make, sphinx.