Teaching

My recent teaching experience comprises two parts: I have been teaching “mini-courses” for summer/winter schools, and participating in some activities in my current university (mostly organizing seminars). This page provides some details on these, along with a full list of my shorter notes that I think might be useful for teaching in one or another way.

Mini-courses

I have designed from scratch and delivered three mini-courses for School for Molecular and Theoretical Biology (SMTB) and Puschino Winter School. Both were aimed at (gifted) high school students and undergrads. They had nothing to do with the high school program, but I obviously needed to exercise some care with respect to prerequisites. Each course comprised four 50-minutes sessions.

“A glimpse into Algorithms.”

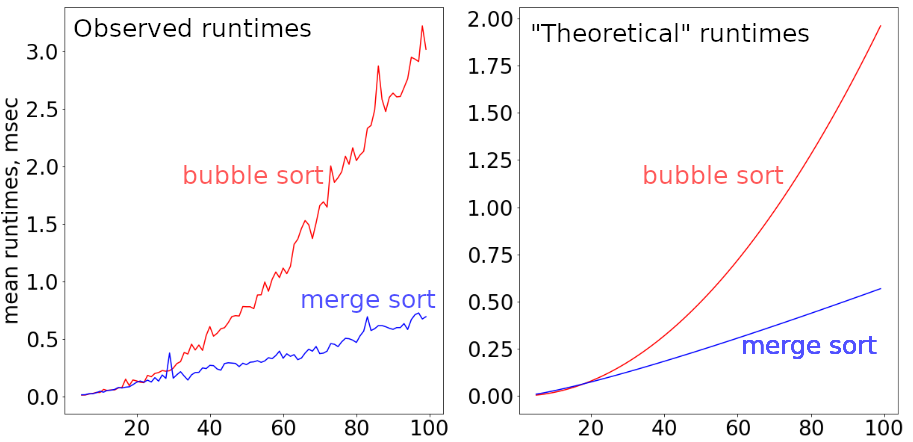
Summary: Introducing and illustrating some key concepts from CS using simple numerical experiments in Python. A crash-course-intro to algorithms and data structures from the computational perspective. E.g., discussing correctness starting from unit tests; asymptotic, best/worst case, and other concepts related to runtime — with measuring actual runtime in seconds using Python’s time module, etc. The purpose was to mention the key ideas, demonstrate that they are (1) not “scary”, and (2) pretty relevant to the practice, even if you are not an (aspiring) computer scientist or a programmer. (This aspect was especially relevant since majority of the students had a background in biology, but was interested in computational aspects as well.)

More details: for syllabus, a few methodological notes, and links to actual teaching materials (slides / jupyter notebooks) see 👉 here.

“Practical Introduction to Probability Theory.”

Summary: This is a theoretical course, i.e., aimed in first place to introduce and discuss the concepts of probability space, random events, independence, random variables, and some others. However, it is presented kind of “backwards”: starting from numerical experiments and trying to “reverse-engineer” the logic behind the math that we actually have in Probability theory. The ultimate goal was to build (together with the students) a usable, practical, but consistent mathematical model of random events.

More details: for syllabus, a few methodological notes, and links to actual teaching materials (slides / jupyter notebooks) see 👉 here.

“How to teach machines: simple examples on ML.”

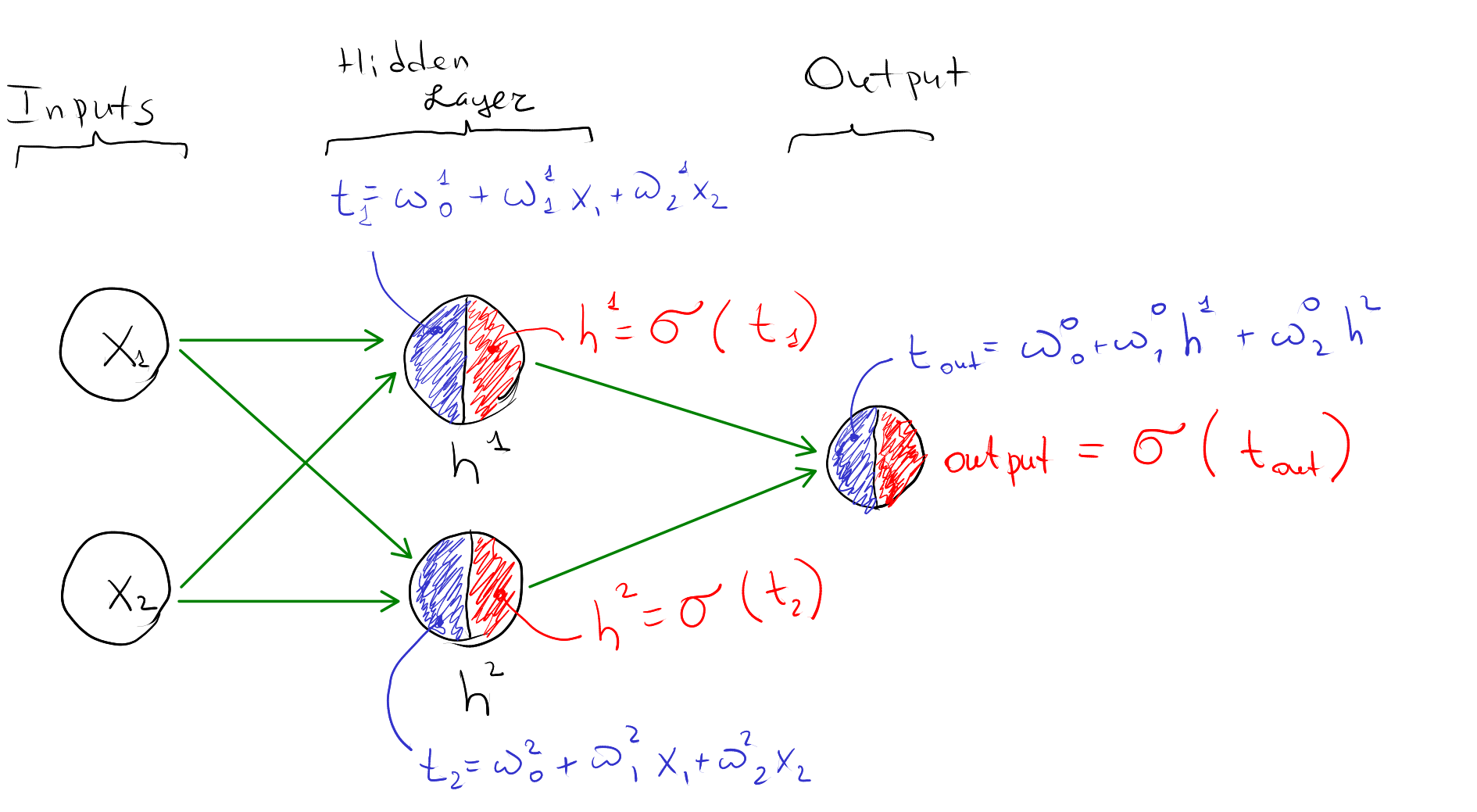
Summary: The idea was to provide a glimpse into ML by discussing three fundamental model types: predicting a number (linear regression), predicting a yes-or-no answer (logistic regression), and predicting… whatever (neural network). Each topic included a simple numerical illustration (such as this three-node network above), and a simple-but-practically-reasonable exercise (such as handwritten number recognition with MNIST dataset, using the same logic, but more neurons and layers.)

More details: syllabus and methodological notes (including teaching materials / jupyter notebooks) are 👉 here.

Seminars at Clemson University

I believe that learning need not necessarily happen in the form of courses, so we have been working with the CU INFROMS Student Chapter on two series of seminars:

• OR Tech Seminar (Spring 2021): discussion of the “researchers' toolbox”. I have presented a series of four one-hour seminars on working with the literature, organizing notes, version control, command line, etc. (more details)
• Journal club on network optimization and interdiction (Fall 2021): we have organized regular meetings, basically, to learn how to read papers and how to do (good) science.

Full index of other “teaching” notes

Below is a complete list of my notes and materials related to teaching. Any feedback / suggestions / corrections are very welcome!