A mind-map for (some) basic OR topics
While I was getting ready for my IE qualifying exams here at Clemson University I needed a big-picture of some basic concepts to “pack” them into my head. So I produced a couple of mind-maps that loosely covered a first-year curriculum – with the intention to make something like a “theoretical minimum” outline. That is, a structured list of topics that might serve as a foundation for PhD research in OR and allow to see the basic coursework structure at a glance. I’d appreciate any feedback on whether the format seems useful and what topics should be included – especially if we’d like to move away from “quals preparation map” towards a “solid theoretical minimum in OR”.
Download
Recommended: git clone the repo with sources, as usual (or just download1 a zip-file). Also, download a Freeplane to open mm-files if you haven’t done so yet (it is free and requires almost no installation, depending on the system). Alternatively:
| Section | Other formats | |
|---|---|---|
| Deterministic OR | 📄 | png, jpg |
| Stochastic OR | 📄 | png, jpg |
A technical note: To me, the most convenient way is to use Freeplane, as it allows to unfold only the nodes you are interested in and keep a conveniently scaled picture on your monitor, like this:
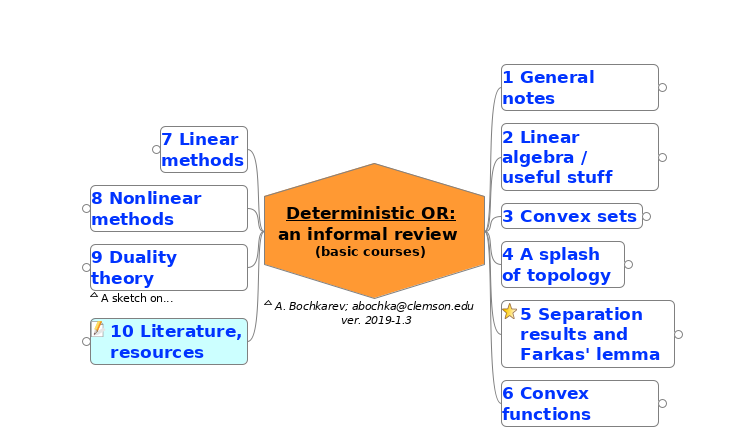
Other than that, PDF seems to be the second best, although you might need some proprietary software for the file to zoom properly2. E.g., I know that it renders and, most importantly, zooms very well on an iPad (but, obviously, does not allow for node folding). If it does not work for you for some reason, PNG and JPG formats are fine, overall, but have some problems with inline pictures in the deterministic part.
What is this?
I just love mindmaps. I find them especially useful for:
- structuring the information – to me, “processing” it this way does help understanding;
- going through to check if I understand and remember everything before the exam (it feels more efficient than just going through the lecture notes);
- checking some specific details later, if I need to.
So I prepared two mind-maps, corresponding to the structure of the IE coursework we had – for the stochastic part and the deterministic part. In terms of presentation, I tried:
- to capture the key results (theorems, corollaries, etc.) that are widely used in the courses – without loss of rigorous notation;
- to provide some notes on applications, interconnections between these results, and sometimes just to summarize them so to see the general idea or high-level logic.
The first part allows to find specific details when needed, the second one – to review the material before the exam efficiently. I sacrificed some exact and formal wording in favor of readability – so I would rather call these an informal reviews, e.g.:
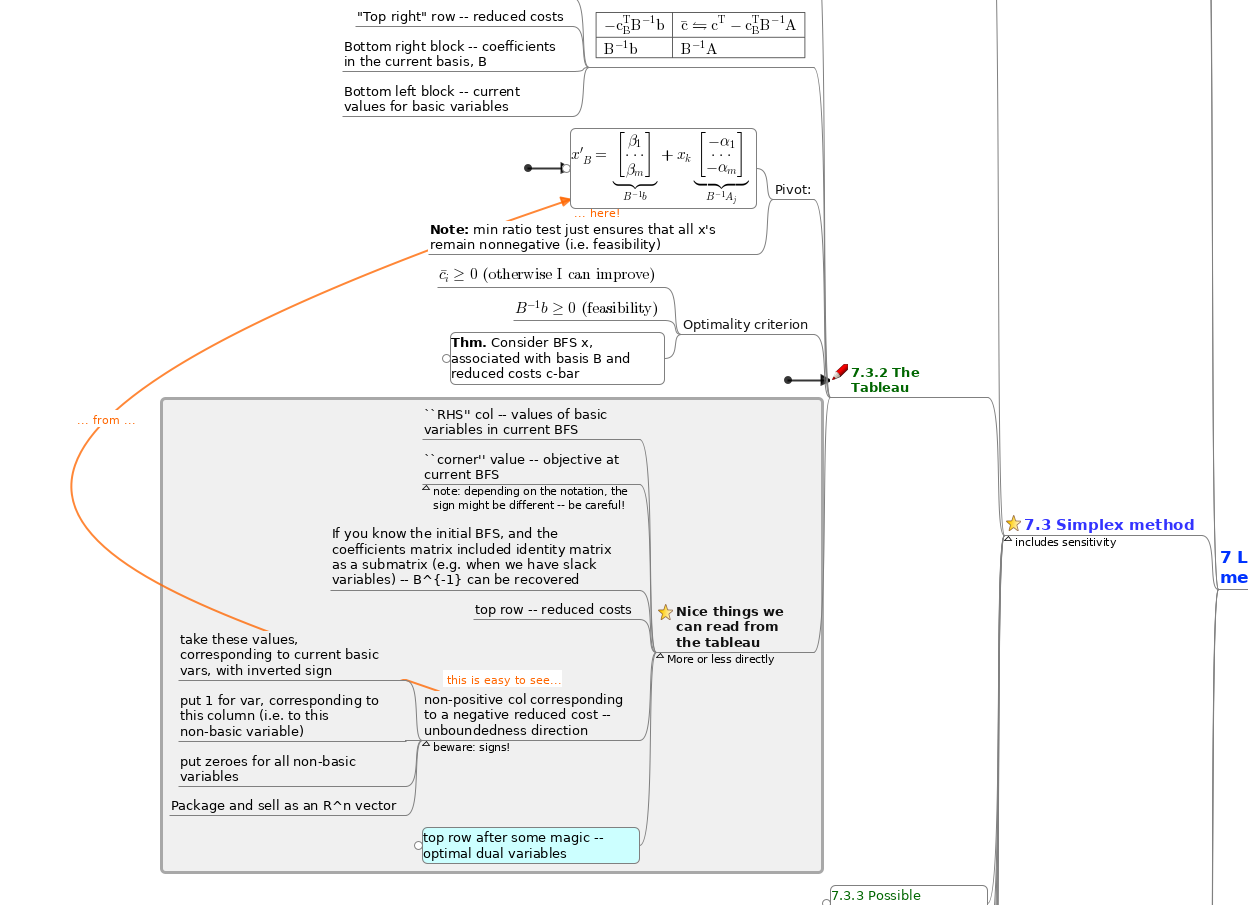
What is not there / potential improvements
There are some parts that I am not really happy with myself. If you think the format itself is useful for your teaching / in the studying process, and you have suggestions / corrections / notes you’d like to be added – albeit connected to the points below or not – please, feel free to drop me an email or even open an “issue” at github.
Besides, there is a separate question whether any other large (and maybe more “mathematical”) topics should be included, as part of an existing map or as a separate diagram – e.g. maybe a separate overview on linear algebra? convex analysis? combinatorial optimization / MiP basics?
Deterministic part
- network flows; there is a large part of deterministic OR that I was not sure how to cover. Going into more details would diverge from the “basic” qualifying exam program and significantly inflate the diagram. Covering less would just… feel wrong;
- dual simplex method; seems like one of the basic topics – include as optional? As non-optional?
- using necessary and sufficient conditions for optimality; despite the fact that I provided couple of summary tables I still have a feeling that some general intuition is missing (that I tried to summarize in these “rules of thumb”). If you know how to formulate it better – please, let me know.
Stochastic part
- set theory – not sure if more details are needed;
- inferential statistics – to me, a very important topic that somehow was covered in passing; hypothesis testing, errors, p-values, model predictive power, etc. etc.;
- queueing models – in fact, are almost not covered. From the other hand, they seem to be analyzed with MCs;
- MDP – Markov Decision Processes basics. Seems to be outside the basic course (but should it?..)